Chaos and markets II

For those who teach finance, a number seems better than no number — even if it’s wrong.

- Mandelbrot and Taleb

It's the Tyranny of the Cookbook, to which we can reply: No number is better than some number - especially when it's wrong.

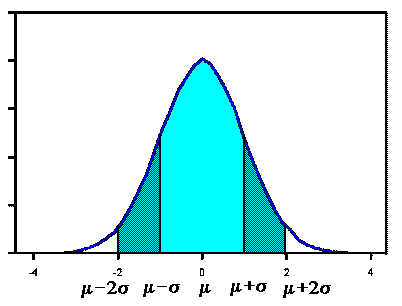
Much financial advice is common-sensical, but in recent decades has incorporated misguided notions of implicitly Gaussian or bell-curve statistics in analysis of price movements, as well as false concepts of "efficient markets." You often hear the jargon of means, variances, and betas. (A beta is just price volatility defined as a second moment, or a variance. The square root of the variance is the standard deviation.) We've already seen a truckload of examples of where and why such concepts break down and why methods based on such assumptions are wrong. The fact that this approach to finance has a Nobel prize is irrelevant.* The methods and concepts have spread from academic finance and economics departments to the desktops and minds of investment specialists in the last 30 years and done significant damage: the Long Term Capital Management crisis in 1998 and the mortgage crisis of 2007-08 were both made possible, in part, by such "professional consensus" malpractice. Here we have legendary cases of Platonified false expertise and the "empty suit" syndrome. The price change distributions are fractal-driven power laws, not bell curves, a fact first presented to the economics world almost 50 years ago by Mandelbrot - and then rejected because it didn't fit convenient, if unempirical, Mediocristan assumptions. The missing practical key is the widely unrecognized enhanced risk of large fluctuations, especially downward moves. Individuals and institutions adopting wrong rules expose themselves unwittingly to much larger risks than they realize.

If we drop the assumptions of bell-curve price fluctuations and efficient markets, where do we stand?

The first is basic math and science: get your units straight. People who practice finance usually get this right, but it's amazing to see ignorance even in the business pages about this. Economics, like mechanics, has three basic types of units: money (a universal store of value and medium of exchange), things or activities (count them distinctly and don't commit the Fallacy of Aggregation, lumping bananas and pork bellies, say), and time. The essential point is that wealth is an accumulation of flows. The flows are prices (measured in money) times things or activities (quantified somehow) divided by increments of time. Interest rates are prices divided by prices divided by time, or just 1/time. Wages are money per unit of labor (an activity) per time. And so on.

The principle of diversification remains, but its rationale changes. It's not "everything will even out" (it doesn't always), but "we don't know very well how individual investments and investment classes will perform - sample all of them." Diversification, not only within investment classes, but especially across classes, is even more important in Extremistan than in Mediocristan.

More basic to the uncorrelated, Gaussian price movement picture is the efficient market hypothesis, which has failed in a number of crucial respects. Market timing matters, especially if you're making large moves (investing or liquidating). The market analysis based on this wisdom is called "technical analysis" or "charting," and its advocates are called "chartists." They stare at price chart patterns. In the "uncorrelated random walk" picture, these patterns mean nothing. But in fact they do mean something. Market moves are indeed correlated across time. Only after three to five years do they start to lose their memory, and it's not clear that they ever entirely do.

Furthermore, there are investment classes that consistently under- and overperform the whole market average. The best-known underperformer is the class of "growth stocks," because they're hyped by the media and analysts to the point where buyers demand them strongly - they're consistently overpriced relative to their long-term performance. OTOH, there are underpriced investments: so-called "value" stocks, for example. Warren Buffet and others have made a fortune hunting for undervalued but worthy investments. It's all boils down to not paying more for an investment than it's worth.

Finally, the "fat tail" phenomenon should make everyone suspicious of probability distribution moments (means and variances). If misanalyzed using Gaussian assumptions, fat-tailed distributions appear to be non-stationary: if you keep sampling such distributions to estimate moments, your results will not, in general, converge as you add more data points. The estimated moments will just keep growing. After an infinite amount of sampling, they diverge to infinity. While means and variances are measures of performance, they're not good measures.

The devil's staircase. A better approach than looking at daily movements is to look at cumulants (integrals) and at absolute linear ranges (price highs - price lows). The cumulant is more stable than the daily changes in value, and sudden jumps in the total value of an asset or flow of goods and services show up clearly. (The fact that such sudden jumps often dominate the total or cumulative history of an asset or market also stands out clearly.) The absolute linear range grows with time, but gives you some sense of the best and worst the market can do. These are the rules of the road in Extremistan. "Mild" variables change by a large number of small increments. "Wild" variables change by a small number of large increments, and "really wild" variables change mainly by a handful of very large increments.

Markets with an incomplete cookbook. The investment community at large still has not fully absorbed Mandelbrot's message about fractals and the uselessness of Gaussian, bell-curve statistics in understanding and prospering in markets. The normal and the Levy-type distributions look similar when you compare them for small deviations from the mean.** It's the large deviations that constitute the acid test, and it is here where investment professionals often start waving their hands.† In a Gaussian world, such large changes shouldn't occur almost ever, and the history of Gaussian markets would be dominated by many, many small changes. But real markets are strongly shaped by a limited set of rare, large, and consequential events. A new investment science to replace the rigorous, Platonified irrelevancies of contemporary financial theory is badly needed.

POSTSCRIPT: Here's a short note on market risk by Mandelbrot and Taleb from a few years ago.

References

= B. Malkiel, A Random Walk Down Wall Street, rev. ed. Classic presentation of efficient-market, Gaussian random walk theory to the masses. Much of the technical side is wrong as a picture of markets, but the basic investment advice (the trade-off between active and passive investment, diversification) is sound.

This posting is a sketch of what's needed to replace the bell-curve price movement framework. Just noted today: the embarrassing underperformance of stock index funds since the 2000 market peak, compared with even lowly bonds, not to speak of value stocks.

= R. Haugen, The Inefficient Stock Market. Nice short, if technical, study of systematic inefficiencies (over- and underpricings) in markets.
---
* Black and Scholes won it in 1997, and Taleb and others have railed against this as a perfect example of rewarding Platonified bullshit with its origins in academic circles, with highly restrictive assumptions, applied to real life where those assumptions don't hold. The LTCM crises occurred less than a year after the award - again suggesting a just G-d, or perhaps one with a refined sense of humor.

A larger objection can be made against the economics Nobel prize altogether, and Taleb and others argue that as well. It's actually a Nobel foundation prize paid for by the Royal Bank of Sweden, not specified in Nobel's will. Although some great and deserving economists have won it (Hayek and Friedman among them), in general, it's difficult to argue with the reality that economics has often been subject to both fads and conveniently cookbook pseudoknowledge. The standards for the Nobel prizes in the natural sciences are much stricter, and I hope they remain thus, so that at least those Nobel prizes mean something.

** Actually, the log-normal. The Gaussian bell-curve is applied, not to prices, but to the logarithms of prices. Small changes in prices are then translated into small percentage changes. (For price P, the differential dP is replaced by dP/P.) For small ΔP's, the log-normal and Lévy-type distributions look almost identical - it is here that the theorists of the Gaussian random walk go astray.

The "random walk" idea can be taken beyond the Gaussian or normal type and recast into a more general form of Lévy flights, dropping the requirement of finite distribution moments. To handle correlations over time between events, it can also be generalized in another way, to have memory: fractal random walks. Such erratic "random" or "drunkard's walks" are an important tool for applying statistical methods to dynamics under conditions of limited knowledge. The random walk is also central to analyzing diffusion (both standard Gaussian and "anomalous" fractal types). In chemistry and biology, the random walk is sometimes called Brownian motion.

† In the last generation, improvisations have grown up around the failure of Gaussian methods, but this series of ad hoc patches and fixes doesn't get to the root of the problem. Some analysts still just take out large deviations ("outliers") by hand, a kind of data denial. Others appeal to the notion of "exogenous" (outside-the-system) shocks, which destroys the method's predictive (if not its retrospective) powers.

The most sophisticated patch is to make the Gaussian parameters depend on time, the common version being GARCH. This is the best you can do within the misguided Gaussian framework; in that wrong framework, the actual (and probably stationary) distribution of price movements looks non-stationary. The time-dependent parameters are supposed to mimic this, but at the cost of largely destroying the method's predictive power.

In the face of chaos or, Chaos casts a shadow

Chaos is the score upon which reality is written.

- Henry Miller

Any natural system, unless proven otherwise, should be assumed to be nonlinear and possibly chaotic. If we can prove it's not linear, we then need to ask, is it chaotic? Under what conditions? If not, under what conditions? Then to move on: can basic degrees of freedom and distinct subsystems be identified? Can their trajectories in time be plotted?

The weather, the state of the Earth's atmosphere, is known to be chaotic, with a Lyapunov time of about two weeks. That is, given anything like our current knowledge of the Earth's weather at any instant of time, weather predictions can be projected out to no more than two weeks, before the forecasts become no better than random guesses.

Financial markets are also known to be chaotic, but unlike the weather, we have no precise, laboratory-controlled fundamental principles to start with. There are many different kinds of financial markets as well. They do seem to lose any distinctive predictability after periods ranging from months to a few years.

What to do? We can't make long-term predictions of chaotic behavior. But chaos is bounded aperiodicity, not unbounded. Over time, it traces out increasingly and ultimately infinitely complex trajectories of temperature, pressure, precipitation, or prices and commodity flows. They're bounded, however, which suggests the notion of a "box" or a "range."

Mathematicians have given us a more subtle and precise version of a "chaos box," called a stable manifold.* Once the periodic and transient behaviors of a system are analyzed and removed from consideration, what's left is the untameable but still boundable meanderings of chaotic motion as it traces out an attractor. The actual record of chaotic trajectories is an infinitely complex fractal, but a stable manifold shadows that fractal in such a way that the manifold does not change over time and the chaotic trajectories don't cross it.**

Such stable manifolds are "chaos captured," to the extent that it can be. They give us a way to take a for-all-time snapshot of chaos without attempting the impossible task of tracing the actual chaotic trajectory for an infinite period.

An earlier posting linked to the stable manifold for the Lorenz attractor, the first modern model of chaotic turbulence arising in the atmosphere. The stable manifold shadows the Lorenz attractor and, being two dimensional, can be converted into a crochet pattern.
---
* "Manifold" is mathematics jargon for a space, like a two-dimensional surface embedded in three-dimensional space, that looks Euclidean locally, but maybe not globally. "Euclidean" means its geometry is the one you learned in high school.

** Mathematicians and physicists say that this object (the stable manifold) is invariant.

Meet the thinkers: The curious aviary of Dr. Taleb

We also know there are known unknowns; that is to say we know there are some things we do not know. But there are also unknown unknowns - the ones we don't know we don't know.

- Donald Rumsfeld

Some of us been waiting for something like this book for a long time, and its Levantine author has come a long way - all the way from the hills of northern Lebanon and the Syro-Greek Orthodox town of Amyoun. The book is The Black Swan: The Impact of the Highly Improbable, and the author, Nassim Nicholas Taleb, former financial trader and now extraordinary professor of the inexact sciences at the University of Massachusetts, Amherst, etc., etc. - essentially, the Dean's pet, and they don't know where to put him. The Black Swan is one of the most important science books for a non-science audience in many years. Like the best chaos and complexity books of a decade or two ago, The Black Swan deals with scientific questions arising from the stuff of everyday life, not far-off galaxies and times long ago.

The core of Taleb's point is the impact of what we don't know, the improbable, and how "randomness" is really another name for our ignorance. But Taleb has a larger target: a whole book was needed to attack and dismantle the legitimacy of bell curve statistics, "Mediocristan" methods wrongly applied to "Extremistan," and explain why so much of the world doesn't follow the "middle of the road" behavior prescribed by the Gaussian-normal distribution and its cousins, such as the binomial or Poisson distributions.

The book is rich with fallacies exploded:

• The Ludic Fallacy. This is the fallacy we pick up when we learn probability based on tightly constrained assumptions, "rule of the game," that make understanding statistical methods based on them as easy as an elementary cookbook. (Ludus is Latin for "game" or "fun.") Real life often presents us with situations of limited knowledge, where probabilistic thinking is appropriate, but where we don't know the "rules of the game," at least not all of them. Many trained in probability and statistics apply the cookbook methods anyway, for the lack of anything better. They capture risk - the known unknowns - but not true uncertainty - the unknown unknowns.
  
  
• The Narrative Fallacy. This is a biggie, practiced on an industrial scale by the news media, every day. We draw connections between dots where the real connections are different, or don't exist, or there are no dots to be found. The news media does it to keep our attention with frequently made-up stories, or "narratives," to use the post-modern jargon, that seem better than no story, or a different one.
  
  
• The Narrative Fallacy supports a related fallacy, one of Misattributed or Reified Intentionality, the fallacy that human society is collectively a result of human intentions or consciousness. In fact, most of it is not, and attempts to force it to be so have led to one disaster after another. Our minds are too limited and possess too narrow a scope of awareness to make this possible. Human society is mostly made behind our backs, so to speak. Taleb's developed views on this question end up very close to the views of the famous Austrian school of economics and sociology.

Taleb has an outrageously funny time explaining what went wrong with statistics and the social sciences in the 19th century, when they were invaded by the concept of the Average Man, and everything was reduced to bell curves, means, and small variations.* All this would hold if our world were Mediocristan. But much of our world is not.

Who's Stan, and what's the difference? Mediocristan is tightly constrained by "fixed totals," or what physicists call "conservation laws." We've already met these and seen what they do. They force the collective behavior into highly restricted patterns, with "equipartitions" of energy, or number, or volume. This certainly is an aspect of our world, and not just in thermodynamics. Heights and weight, for example, both of them strongly limited by gravity and metabolic limits, are distributed in a way close to the bell curve. But then again, consider the distribution of weights in aquatic animals, and you can already see: without gravity, the maximum size is much bigger (think of whales and octopi).

The key to Mediocristan is the Central Limit Theorem. If a population's distribution (of whatever attribute) is made up of independent instances and has well-defined moments (weightings), then the distribution approaches the bell curve in the limit of "large numbers." The presence of "fixed totals" guarantees well-defined distribution weights (moments).

But in many, perhaps the majority of, cases, it fails. The instances are not independent of one another, not distributed with well-defined weights, or neither. The distribution then has much less reason to clump near the mean. In fact, in such cases, many of our usual statistical clichés (means, variances, medians, etc.) fail to capture what's going on.

This is the world Taleb calls Extremistan.** If there's no "fixed total" of something being distributed (like economic wealth, or the total number of books sold by a single author, say), there's no reason to think that the total will be broken up in a roughly even way among instances. Here is the key to understanding much of our world - economic markets, wealth, and income in particular. Many days on markets are boring. Some are interesting. A few are extraordinary - and it these days, the black swans of the financial world, that end up dominating the cumulative history of the market. Just look at the last few months' newspapers.

We encounter similar truths in biological evolution, in contrast to the anodyne but wrong gradualism still dominantly taught. Most of the cumulative change in biological evolution is due to a small number of extraordinary turns of events that have outsized impacts echoing through the millennia. Ditto for human history.

And of course, on Taleb's home ground of financial markets, the reality of black swans, and fractal or fat-tailed distributions, is of intense interest. The disastrous application of bell curve-based statistical methods to quantitative finance in the last generation has not made markets better-behaved or investment strategies sounder. On the contrary: the 1998 Long Term Capital Management and 2008 mortgage crises make clear just how wrong these methods are. They're "state-of-the-art" in some sociological sense, but it's a mistake to call them an art, much less a science.

We've met these strange birds already: Taleb's black swans are the stream of unique events of chaos. His grey swans are those occasional, semi-tamable events at the low frequency end of the spectrum.

Plato in Nerdistan. As the book develops in its middle, Taleb wanders through the thickets of epistemology, how we know what we know. This part is somewhat weaker than the book's earlier and last parts, because the argument goes too far afield and loses a bit of focus. Taleb over-blurs the distinction between event (his specialty) and entity. Before European explorers reached Australia, they believed that all swans are white. The whiteness was not an essential part of the definition of "swan," nor was the belief obviously false. It was a contingent statement about two different properties of things: "swanness" and "whiteness." This supposed connection met its end when the explorers encountered the black swans of Australia. A deeper lesson took a longer to sink in, and some still resist it: disproving something is much easier than proving it. Proving something requires understanding its nature more deeply and thoroughly than our knowledge often runs.

Even this middle part is rich with deserving targets. Taleb calls them "Platonified abstractions," the stuff of academic knowledge. They're thrown around confidently by people who don't know what they don't know. This might almost be a definition of nerdity: what you know fits into cut-and-dried abstractions, and you confuse these with the actual world only known to us very imperfectly. Nerds stand in counterpoise to Taleb's foil, the Fat Tonys, the proverbial cabdrivers of the world who know better and who understand that when it comes to Platonicity, you can take it or leave it.

What do you know, and how do you know it? Exact human knowledge is coined under laboratory control or by precise logic. Most of the knowledge we use in everyday life is approximate knowledge in well-defined, if not controlled, conditions. At the edges of what we know is amorphous knowledge, often mixed in with a lot of prejudice and guessing. And if we want more and better knowledge, we face the reality of trade-offs. I can be sure something will happen today, but I don't know its significance. I can also be sure something significant will happen in the next year, but I don't know when.

Modern science is not based on induction, contrary to common belief. It's based on a mixture of hypothesis, deduction, controlled experiment, and controlled mathematics. It's not because scientists are dogmatists that they live by deduction. It's because deduction allows one's reasoning to be kept under precise control, with all the assumptions on the table and the steps clear. Induction (like statistical correlation) can certainly be strongly suggestive of hypotheses, and it's essential for developing logical definitions. But you can't prove anything with it. One counterexample - the black swan - destroys it. Silent evidence is always lurking to upset the induction cart.

The essence of probability. Coping with limited knowledge means falling back on probabilistic arguments, and this is in fact the origin of statistics. Its modern founders (Pascal, Bayes, Laplace, Gauss) all identified probability with a greater or lesser sense of certainty about something, not its frequency. This distinction fueled a great 19th-century debate between Bayesians and frequentists. Until the 1920s, the frequentists had the upper hand. But modern mathematics has abandoned frequentism, except as an approximation in carefully circumscribed situations where the Ludus isn't a Fallacy (like sports or gambling, for example). With frequentism came many long-unexamined false assumptions; for example, that "noise" and "randomness" are "theory-free" concepts. In fact, few things are more loaded down with theoretical assumptions than "randomness," if taken as a metaphysical category. Taking it as a statement about the limits of human knowledge, OTOH, makes it almost a truism. In most cases, the Ludic Fallacy will come back to bite us: we often don't know all of the rules of the game.

Unfortunately, the frequentist approach to statistics is still taught because it's cookbook. Even in situations where a canned approach is not appropriate, a recipe feels comforting, relieving people of having to think. I might even call this the Cookbook Fallacy: having a wrong recipe is better than no recipe. Actually, no recipe is better than a bad one - at least it's honest and doesn't force us into wrong assumptions.

Taleb in his garden. Along with his skeptical empiricism, Taleb exhibits other exquisitely refined scientific tastes, paralleling his capacious gourmand tastes in literature and food. This might seem an affectation, but it points to an important truth.

Richard Feyman, another man of powerful scientific intuition, said: to do good science, you gotta have taste! Science, like the arts, has its forms of kitsch: rules mechanically applied without the imagination and drive for the fully worked-out development, but without indulging in useless repetition. Science is still and will always remain partly an art. To have taste is to avoid weak arguments and rationalizing, and to avoid applying methods and concepts where and when they are not valid. It is to think that, if there's no deep fundamental principle that prevents something, then why not? What would the world look like if it were so? Maybe you lack the imagination to see that that is our world. Taste is seeing that not taking obvious things for granted is a true royal road to discovery. It is paying attention to the silent evidence, to the dog that didn't bark, and to the pious who prayed and drowned anyway: survivor bias.

Taste in science also requires revisiting fundamental issues, ones never completely resolved. The progress of science has solved many problems defined more narrowly. But deep issues remain, even if transformed. Science has its classics and its literature, history, and philosophy; progress doesn't erase their importance. Read them and avoid being a cultural philistine.†

Taleb reminds us that what we don't know can hurt us, and that what we don't know is often more important than what we do. The Black Swan is a fine book. Buy, read, and enjoy it, patiently and slowly. And if nothing else, be charmed by the bittersweet tale of Yevgenia and her unknown masterpiece.
---
* Hayek attacked much the same in his Counterrevolution of Science, laying out the 19th-century origins of Platonified pseudo-knowledge in the social sciences and the pretensions of social planning that often went with it. Plenty of perceptive people, like our old friend Poincaré, resisted this development, this misapplication of inappropriate mathematical methods to society. But the Tyranny of the Cookbook is an unrelenting one.

** Not to be confused with Wackistan. That's where Ahmadinejad lives.

† Taleb uses the German term, Bildungsphilister, just to show, I suppose, that he isn't one.

Be alert to a real affectation, indulging in philosophical problems isolated from anything real. As Taleb points out, most philosophical issues worth bothering with are suggested by something outside philosophy.

Chaos is weakly constrained

You can have chaos with as few as two degrees of freedom in a closed system, and with only one if the system is "pumped" from the outside. But much of the chaos around us is a result of systems with many degrees of freedom. Such systems, whether open or closed, are often analyzed with statistical methods: statistical physics, or statistical mechanics, from which we get statistical distributions, averages, variances, and all the other paraphenalia. In physics, the distributions and their moments (the generalized weights of the distribution - the mean and variance are the first two) are fixed by general conservation laws, such as the conservation of the number of bodies (or particles) and of the energy in the system.

If we look at each changing degree of freedom in detail, such conservation laws tend to reduce the overall chaos in the system. The more conservation laws, the less chaos. Each conservation law is related to a symmetry of the system: the dynamics of an isolated system is invariant in time for example and leads to a conserved total energy; if the identity of its constituent parts is unchanging, the number of particles is conserved too. Non-chaotic systems - the standard ones in physics being a single planet orbiting a star (or one electron orbiting a nucleus) and a simple harmonic oscillator - have so much symmetry that their motion is non-chaotic and can actually be solved for exactly with pencil and paper (in closed form). This is an unusual property in general; most systems cannot be so solved, most are nonlinear, and many are chaotic. Chaos is the norm; nonchaotic motion the exception. A few conservation laws still hold rigidly, but they are far too few to place much constraint on the motion of a system of many degrees of freedom.

Consider a modest volume of air in the room, a mole, with about 10²⁴ molecules (1 followed by 24 zeros). The constraints imposed by conserving their total energy, total volume, and total number place three restrictions on the degrees of freedom of the gas: six times the number of molecules. It's "six" because each molecule can translate in three separate directions and rotate its orientation in three independent ways.

If we don't follow each degree of freedom in detail and instead fall back on a statistical description, the conservation laws announce themselves in a different way. For each conserved total quantity (energy, number, and volume, say), a statistical distribution results whose properties are fixed by that total. Energy is the best-known; its distribution is controlled by a parameter equivalent to temperature. Furthermore, a not-totally-strict, but very restrictive, type of "equal distribution" of energy among the individual particles results (equipartition). It's very unlikely that the particles will share the fixed total energy in any way other than sharing it equally. Similarly for fixed total volume (giving rise to pressure, as particles bounce off the walls that constrain them to remain in that volume) and fixed total number (giving rise to chemical potential, the "energy cost" of introducing or removing one particle from the system). These laws are the reason, for example, why it is overwhelmingly unlikely that the air in the room I am sitting in right now will find itself all crammed in one corner, leaving the rest of the space a vacuum. And that's a good thing.

But we can measure an infinity of other properties about the system, and, in general, the answers will not be constrained by a conservation law. In that case, the particles aren't sharing a fixed total of something. The resulting patterns of some such variable, in general, are chaotic and generally exhibit a wide range of possible "sharing schemes." The statistical distributions that result will look nothing like the "law of large numbers" or equipartition world just outlined for the conserved case. Instead, they will be distributed according to a fractal, or scaling, law, one that is self-similar on many scales. For a truly chaotic system, after waiting an infinite amount of time, the distribution would be a perfect fractal, looking like itself no matter if you zoom in or zoom out. It's utterly different from the sharply-defined world of averages and small deviations defined by conservation laws.

We'll meet this distinction - a world of averages versus of a world of scaling - again, when we consider the statistical nature of chaos and take a look at a remarkable new book.

Strangely attractive

What is that infinitely complex, non-repetitive structure that chaos lays down? Where does all that complexity come from?

Any depiction of chaotic motion necessarily has been generated by observing or calculating a finite elapsed time of motion. So no picture of chaos can ever show its full complexity. An infinite amount of nonrepetitive motion accumulates inside a finite box after an infinite time. And it takes that infinite time to fully exhibit the complexity of the motion. If the motion could be fully executed in any finite time, it would start to repeat on longer times. It wouldn't be chaotic.

A recorded chaotic trajectory of infinite time is called a strange attractor. It's an attractor because the motion doesn't leave the box. It always "sticks around," even as it never repeats. Mathematicians call it strange because of that infinite complexity. Strange attractors are also fractals; that is, objects with infinitely nested self-similarity.

The most famous strange attractor is that one from the first modern investigation of chaos, the Lorenz attractor, named for the man who discovered it.

The fractal concept is more general and has applications in many areas of applied mathematics. They were first discovered in the late 19th century, but not popularized until Mandelbrot brought them to the world's attention starting in the 1960s, showing that such structures are ubiquitous in the natural world.* Here are two.

This is the Sierpinski triangle.

This is a Julia set.

(If this picture reminds you of a spiral galaxy or a starfish, that's not an accident.)

---

Where does all that infinite complexity come from? Such structures, by not representing something repetitive, seem to have encoded in them an infinite amount of information. How can that happen?

It's our old friends, the irrational numbers, again. A rational number, being a ratio of integers, contains a finite amount of information. If you decimal-expand a fraction, that decimal form will eventually start to repeat, indicating that a rational number has "nothing more interesting to say" after a finite number of digits.

43/11 = 3.9090909.... , or 89/65 = 1.369230769230769230769.... .

Not so an irrational number. Its decimal expansion never repeats. The square root of 2 is irrational.**

= 1.41421356237309 ....

"Never repeats" - sound familiar? It should. It's the essential characteristic of chaos: bounded nonrepetition. Chaos "processes" the infinite amount of information in the continuum of irrational numbers into infinitely detailed structure, but takes an infinite time to do so.

POSTSCRIPT: Learn more about chaos and the people who discovered it from one of the classics of modern science, James Glieck's Chaos: Making a New Science (1987).
---
* Fractals have even become a basic element of realistic computer graphics today, allowing the creation of much more realistic clouds and landscape, for example, than anything based on those boring old Platonic shapes of spheres, boxes, and so on. All thanks to Benoît.

Chaos was also first discovered in the late 19th century, by the French mathematician Poincaré. Based on his study of irregular planetary orbits, he was able to imagine the infinitely filigreed complexity of the strange attractor. But the terminology and true import of chaos had to await the 1960s and advent of the electronic computer. Then mathematicians and physicists could really investigate the complex subtleties of chaos and let computers do all the calculational drudgery of the necessary arithmetic.

In the 1950s, the Italian-American physicist Fermi, after an encounter with an earlier forerunner of chaos, referred to the study of linear systems that so fills up science and engineering education as the study of "elephant animals." Everything else was "non-elephant animals" - that is, most animals - and he wondered why we didn't spend more effort studying all those non-elephants.

** The square root of two is the first number known to be proven to be irrational. That is, it cannot be represented as the ratio of two integers. For several proofs, see here.