Strangely attractive

What is that infinitely complex, non-repetitive structure that chaos lays down? Where does all that complexity come from?

Any depiction of chaotic motion necessarily has been generated by observing or calculating a finite elapsed time of motion. So no picture of chaos can ever show its full complexity. An infinite amount of nonrepetitive motion accumulates inside a finite box after an infinite time. And it takes that infinite time to fully exhibit the complexity of the motion. If the motion could be fully executed in any finite time, it would start to repeat on longer times. It wouldn't be chaotic.

A recorded chaotic trajectory of infinite time is called a strange attractor. It's an attractor because the motion doesn't leave the box. It always "sticks around," even as it never repeats. Mathematicians call it strange because of that infinite complexity. Strange attractors are also fractals; that is, objects with infinitely nested self-similarity.

The most famous strange attractor is that one from the first modern investigation of chaos, the Lorenz attractor, named for the man who discovered it.

The fractal concept is more general and has applications in many areas of applied mathematics. They were first discovered in the late 19th century, but not popularized until Mandelbrot brought them to the world's attention starting in the 1960s, showing that such structures are ubiquitous in the natural world.* Here are two.

This is the Sierpinski triangle.

This is a Julia set.

(If this picture reminds you of a spiral galaxy or a starfish, that's not an accident.)

---

Where does all that infinite complexity come from? Such structures, by not representing something repetitive, seem to have encoded in them an infinite amount of information. How can that happen?

It's our old friends, the irrational numbers, again. A rational number, being a ratio of integers, contains a finite amount of information. If you decimal-expand a fraction, that decimal form will eventually start to repeat, indicating that a rational number has "nothing more interesting to say" after a finite number of digits.

43/11 = 3.9090909.... , or 89/65 = 1.369230769230769230769.... .

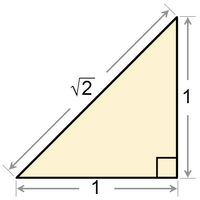
Not so an irrational number. Its decimal expansion never repeats. The square root of 2 is irrational.**

= 1.41421356237309 ....

"Never repeats" - sound familiar? It should. It's the essential characteristic of chaos: bounded nonrepetition. Chaos "processes" the infinite amount of information in the continuum of irrational numbers into infinitely detailed structure, but takes an infinite time to do so.

POSTSCRIPT: Learn more about chaos and the people who discovered it from one of the classics of modern science, James Glieck's Chaos: Making a New Science (1987).
---
* Fractals have even become a basic element of realistic computer graphics today, allowing the creation of much more realistic clouds and landscape, for example, than anything based on those boring old Platonic shapes of spheres, boxes, and so on. All thanks to Benoît.

Chaos was also first discovered in the late 19th century, by the French mathematician Poincaré. Based on his study of irregular planetary orbits, he was able to imagine the infinitely filigreed complexity of the strange attractor. But the terminology and true import of chaos had to await the 1960s and advent of the electronic computer. Then mathematicians and physicists could really investigate the complex subtleties of chaos and let computers do all the calculational drudgery of the necessary arithmetic.

In the 1950s, the Italian-American physicist Fermi, after an encounter with an earlier forerunner of chaos, referred to the study of linear systems that so fills up science and engineering education as the study of "elephant animals." Everything else was "non-elephant animals" - that is, most animals - and he wondered why we didn't spend more effort studying all those non-elephants.

** The square root of two is the first number known to be proven to be irrational. That is, it cannot be represented as the ratio of two integers. For several proofs, see here.