What comes around

As promised, some exploration of cycles in nature.

The point of cycles is that much of what we experience in the world is apparently periodic. Things repeat, although complex things have parts that repeat at different frequencies. This posting explains these terms - periodic, frequency, and related ideas. It starts a train of thought culminating in an attempt to define all natural motion as a combination of periodic motions, the failure of that attempt, and the consequences of that failure.

To start, any system you pick has to be broken down into its most basic parts. The elementary ways that the parts - molecules, atoms, rigid pieces that move as a unit - of such systems - a bouncing ball, a rolling car, air vibrating with sound - have to be identified. These elementary possible motions are called degrees of freedom and can represented as mathematical variables. When they move in time, these variables are functions of a master variable, time, as measured by a clock or some other time-keeper.

These degrees of freedom can move in lots of ways, depending on the forces acting on them. A powerful way to think of its motion is to start with the most basic of periodic motions, simple harmonic oscillation. The harmonic part is related to musical pitch or tone, a point we'll come back to. Simple harmonic motion is also the small-amplitude swinging of a pendulum, or the oscillation of a spring, if it's not deformed too much.

Harmonic oscillation is elegantly defined by projecting constant circular motion on to a line.

1. Start with a circle. Mark a point on its edge. Let the circle turn at a constant frequency f, with the mark returning back to its start every period T = 1/f. If the unit of T is the standard seconds, then the unit of f is hertz (Hz or inverse seconds).
   


2. We're used to measuring angles with degrees, with 360 degrees (360^o) for a full turn. This isn't the natural way to measure angle; the right way is radians, which is the arc length of the circle traced out by a circular radius R turning through the angle theta: θ = arc length swept out/radius. Then a full turn is θ = 2πR/R = 2π radians. Notice that, in this definition, the length scale of the circle (the radius) cancels out in the ratio, as it should. Angle is independent of size.
   
   
3. Now project the uniformly turning motion of the mark on the circle onto a line tangent to the circle. At any instant, the projected linear length is a trigonometric function of the angle swept out. The function is one of those you learned in high school, a sine or cosine, depending on how you do the projection. In this drawing, these functions are defined in the usual way, by the sides (a,b) of a right triangle in ratio to the triangle's hypotenuse (c). Because of the Pythogorean theorem, a² + b² = c², the trigonometric functions are not completely independent. For any angle θ, they satisfy sin²θ + cos²θ = 1.
   
   
4. Graphing functions of time, we get the standard sine and cosine waves. The combination ω = 2πf = 2π/T is called the angular frequency. The angle swept out is θ = 2πft. After one period t = T, the angle swept out is θ = 2πfT = 2π, a complete circle in one period. The elementary motion is the sine or cosine: sin(ωt) or cos(ωt). The thing in the parentheses (ωt) is the argument of the function.
   
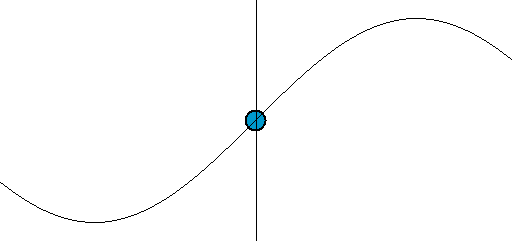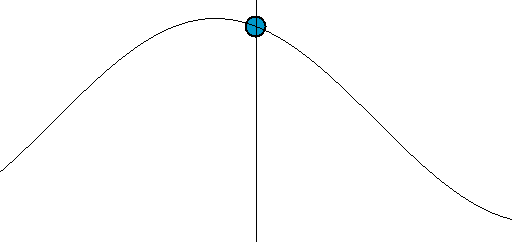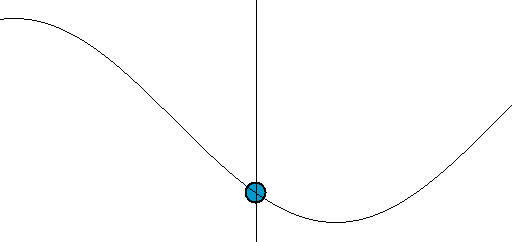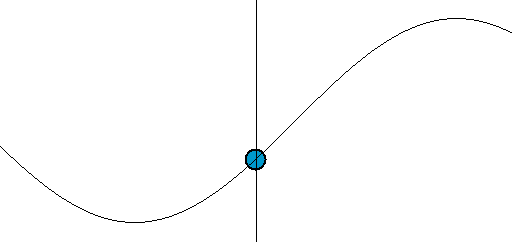
   The shape of sine and cosine are identical, just shifted in argument by 90^o or π/2 radians. Such shifts in the argument are phase differences or phase shifts. We won't talk much about phase now, but it will come back when we talk about real cycles in climate. Phase is usually represented by φ; it's related to a time shift by dividing out by ω or 2πf. Unless phase is important, we'll just stick to one trigonometric function (say, sine).

All simple periodic motions need just three numbers for their complete definition:

• Frequency f (or angular frequency ω or period T),
• Phase φ (which we'll mostly ignore),
• Amplitude (the oscillation's maximum positive size, which also, by symmetry, gives its most negative size).

Multiperiodicity and commensurability. Can motions of different periodicity be combined? If they're two possible motions of the same degree of freedom, yes. The combined motion no longer oscillates at a single frequency. (If this is about sound, it's the combination of two pitches.) Peculiar properties of the trigonometric functions lead to an important conclusion: the combination of two harmonic oscillations is a third, different oscillation (at the average of frequencies, (f₁ + f₂)/2) whose amplitude is multiplied or modulated by an envelope of "ghost" oscillation (at the half-difference of frequencies, |f₁ - f₂|/2). The modulation envelope is often called the heterodyning or "beating" of two frequencies against one another.*

In music, "beating" is pleasing or grating to our nervous systems depending on whether there's a simple, low-order integer relationship between the frequencies - like 1:1 (exact consonance), 2:1 (octave), 3:2 (fifth interval, or dominant-tonic), etc. - or not. More dissonant combinations are higher-order integer pairs, like 9:7 or 13:11.

If we combine many "pure" frequencies f_i (with the index i labeling each frequency), the resulting motion no longer has any simple oscillatory interpretation. Even in the two-frequency case, the period of the summed frequencies (1/T = 1/T₁ + 1/T₂) is not a true period, because of the modulation at the difference or heterodyning frequency. It's not hard to see that the motion can repeat only if the two frequencies have a ratio of two integers (m,n) - that is, the ratio of frequencies has to be a rational number m/n (assuming common factors have been canceled - the two integers are mutually prime). If this is true,

f₁/f₂ = m/n = T₂/T₁, so that mT₁ = nT₂

In that time mT₁ = nT₂, m cycles of oscillation 1 = n cycles of oscillation 2, and the combined motion repeats. The two frequencies are said to be commensurate.

If the ratio of frequencies is not a rational number, the frequencies are incommensurate, and the overall motion never repeats. This fact has profound consequences, as we shall see.

The ultimate goal of introducing periodicity is to see if all change can be analyzed into combined simple harmonic motions. The answer is no, but it's "almost" true. The power of such methods and the limitations imposed by the "almost" are critical for understanding cycles of climate and heavenly bodies - and any other sort of cycle.
---
* This how AM radio works. The modulation frequency is a very small frequency in the audible range (few 100 Hz up to about 10,000 Hz) and comes from the difference of two very large and very close radio frequencies (millions of hertz, or megahertz, MHz).